一 起源
在原创开发作者相关功能的时候,遇到了一个文本对比的功能,需要向作者展示章节内容修改前后的差异:作者会对章节内容进行修改,后台审核过程中,也会对章节内容做一定的调整,这些调整的细节,需要告知作者。
实现一个 diff 的功能,这需要解决两个问题,核心问题是如何寻找出两段给定文本的差异,次要问题是如何保存数据。
首先,如何找出两段文本的差异? 当时调研后发现有个现成的 PHP 扩展,可以实现这一功能,但无法很好的解决问题,会有以下不足:
- 扩展依赖底层库
xdiff.h,默认是按行对比。我们对小说章节文本内容进行存储时,会带上<p>标签来进行分段,而不是系统换行符,那么整个章节的 内容都会被视为一行,对比结果会退化为两段文本是否一致,无法体现修改的细节。而修改分段方式会涉及到业务的调整,引入更多的不确定性。 - 扩展非官方扩展,以扩展的方式使用,需要自己编译安装,影响运行环境的标准化,引入额外的不确定性。
因此决定这部分自己来实现。
其次,关于如何保存数据? 方案一:保存每次修改前后的完整内容。优势在于处理起来方便,对原有流程的入侵比较少;缺点在于冗余内容比较多,每次修改都要保存一个完整的历史备份, 而且每次展示差异,都需要重新执行一次对比。
方案二:在每次修改时找出修改前后的差异细节,仅对差异的细节与最后一次的内容做保存,那么章节的历史版本内容都可以根据最新内容加上差异的细节反推出来。 优势在于冗余数据少。但有个比较明显的缺陷,需要保存连续的差异记录,如果中间某次差异记录的丢失,会导致往前所有的记录无效。
我们选择的是方案二。
二 diff实现的探索
2.1 LCS最长公共子序列
最长公共子序列算法 LCS 是实现文本对比的手段之一,他的原理就是找出两段给定文本的公共子序列中长度最长的序列,也就是相同的部分, 那么剩下的就是两段文本间的不同部分。想要找出这个最长的序列,可以通过动态规划的方法,如果把要对比的两串文本表示为X,Y,他们的最长公共子序列为 Z:
X=<x1,x2,x3,x4...,xm>
Y=<y1,y2,y3,y4...,yn>
Z=<z1,z2,z3,z4...,zk>
则可以将这个过程表示为 LCS[X,Y] = Z,假设对于XY各有一个子串Xi,Yj,他们的公共子序列表示为 LCS[Xi,Yj]
X=<x1,x2,x3,...xi,xi+1...,xm>
Y=<y1,y2,y3,...yj,yj+1...,yn>
那么当 Xi,Yj 各自再增加一个字符的长度时,LCS[Xi+1,Yj+1] 如何取值呢?
- 如果
xi+1 = yj+1,说明LCS[Xi+1,Yj+1]和LCS[Xi,Yj]相比,新增了一个相同的字符,所以LCS[Xi+1,Yj+1] = LCS[Xi,Yj] + 1 - 如果
xi+1 != yj+1,那么LCS[Xi+1,Yj+1]就是LCS[Xi+1,Yj]和LCS[Xi,Yj+1]中比较大的那一个, 即LCS[Xi+1,Yj+1] = MAX(LCS[Xi+1,Yj],LCS[Xi,Yj+1])
上面的描述,就是通过动态规划解决这个题时,所要找出的状态转移方程,用代码表示,就是:
$X = ['A', 'B', 'C', 'D', 'A'];
$Y = ['A', 'C', 'B', 'D', 'E', 'A'];
$m = count($X);
$n = count($Y);
$dp = [[0]];
for ($i = 0; $i < $m; $i++) {
for ($j = 0; $j < $n; $j++) {
if ($X[$i] == $Y[$j]) {
$dp[$i][$j] = (isset($dp[$i - 1][$j - 1]) ? $dp[$i - 1][$j - 1] : 0) + 1;
} else {
$dp[$i][$j] = max(
(isset($dp[$i - 1][$j]) ? $dp[$i - 1][$j] : 0),
(isset($dp[$i][$j - 1]) ? $dp[$i][$j - 1] : 0)
);
}
}
}
经过状态转移方程的反复求解,就计算出最长公共子序列的长度,这个过程可以通过画表来清楚的表示,表格如下图所示,完成这个表格就完成了目标的一半, 然后只需要反过来,如图中红线所示,寻找处这样一条路径,就得到了最长公共子序列的具体字符:
- 箭头斜着走,说明当前字符是属于最长公共子序列的,也就是相同的部分
- 箭头往上走,说明当前字符属于纵向的字符串,新增的部分
- 箭头水平走,说明当前字符属于横向的字符串,删除的部分
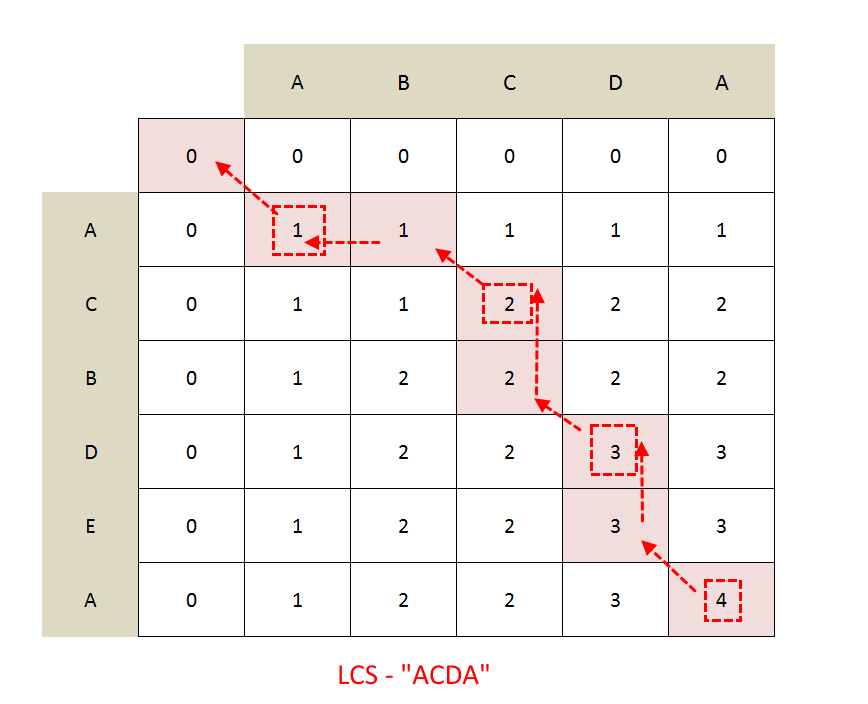
虽然这个方法可以很直接的进行 diff,但是,这个算法的空间时间复杂度都是 O(m*n),当对比的数据规模变大时,所耗费的时间与内存会上升的非常明显,性能急剧下降。 而另外一种实现,Myer差分算法,可以一定程度的解决性能问题,其特点是最长公共子序列越长,性能消耗越小。
2.2 自己造的轮子
其实,怀着优化性能的心态,我也尝试过自己来解决这个问题:既然对过长的内容做 LCS 性能不佳,那我们试着去控制比较的规模不就可以了?
比如在 X 中取一个固定长度的子串 A ,然后在 Y 中搜索一下,如果命中了,说明两个字符串有这样一个相同的子序列,然后以这个子串为基准, 检查后面的字符是否相同,当检查到结果为不同时,得到相同的字符串 AB ,重复这一过程,这样就能找出相同片段 AB 和 E, 以及差异片段 C 和 D,此时 CD 的长度规模和原文本相比,就被缩小了,可以使用 LCS 算法来进一步计算出差异片段的细节。
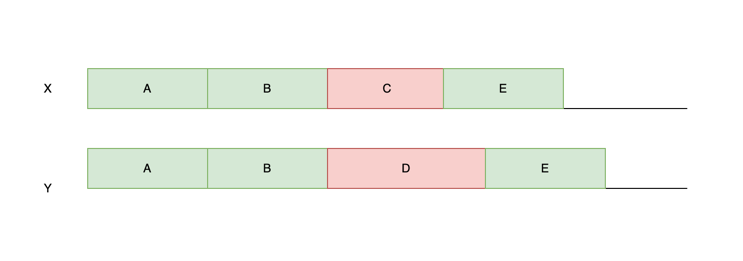
通过上述过程,可以找出 X 与 Y 中的相同片段与不同的片段,基本实现 diff 的功能。 只是会有几个问题:
- 这样获得的结果,"正确性"会低上很多,因为搜索的过程中,相同区域可能会命中两个,而我们没有额外的信息,来支撑我们判断哪个更正确。
- 如何确定这个"固定长度"?这个固定长度取太长则会降低命中率,达不到缩小规模的目的;取得太短,命中率变高,取到最优解的概率低,降低准确率。
2.3 google算法
上述两个包也是关于 diff 的实现,实现上大致会有以下步骤:
- 首先去掉两段文本首尾相同的部分,继续对比剩余的部分。
- 取较长文本的四分之一处或二分之一处,长度为四分之一的文本s,到较短的字符中进行查询,看能否命中。
- 如果能,则继续往前、往后判断文本的内容是否也相同,是则追加到文本s,直到两端都不相同。
- 看其完整长度是否超过较长文本的一半,如果是则标记为相同。
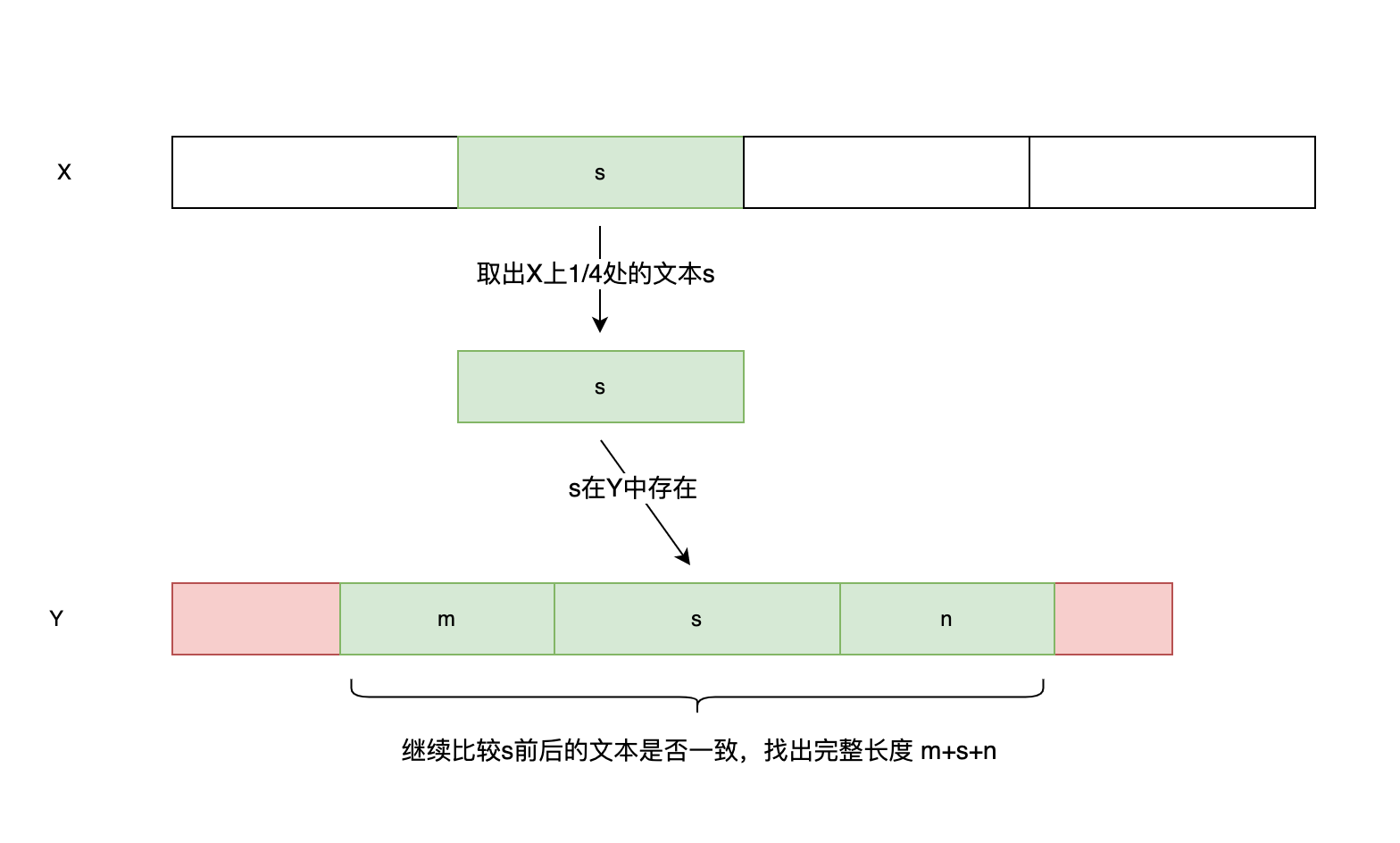
通过注释,我们知道这是一个关于快速 diff 的策略,那么他为什么要这样来实现,又有何依据呢?
较长字符串的半长
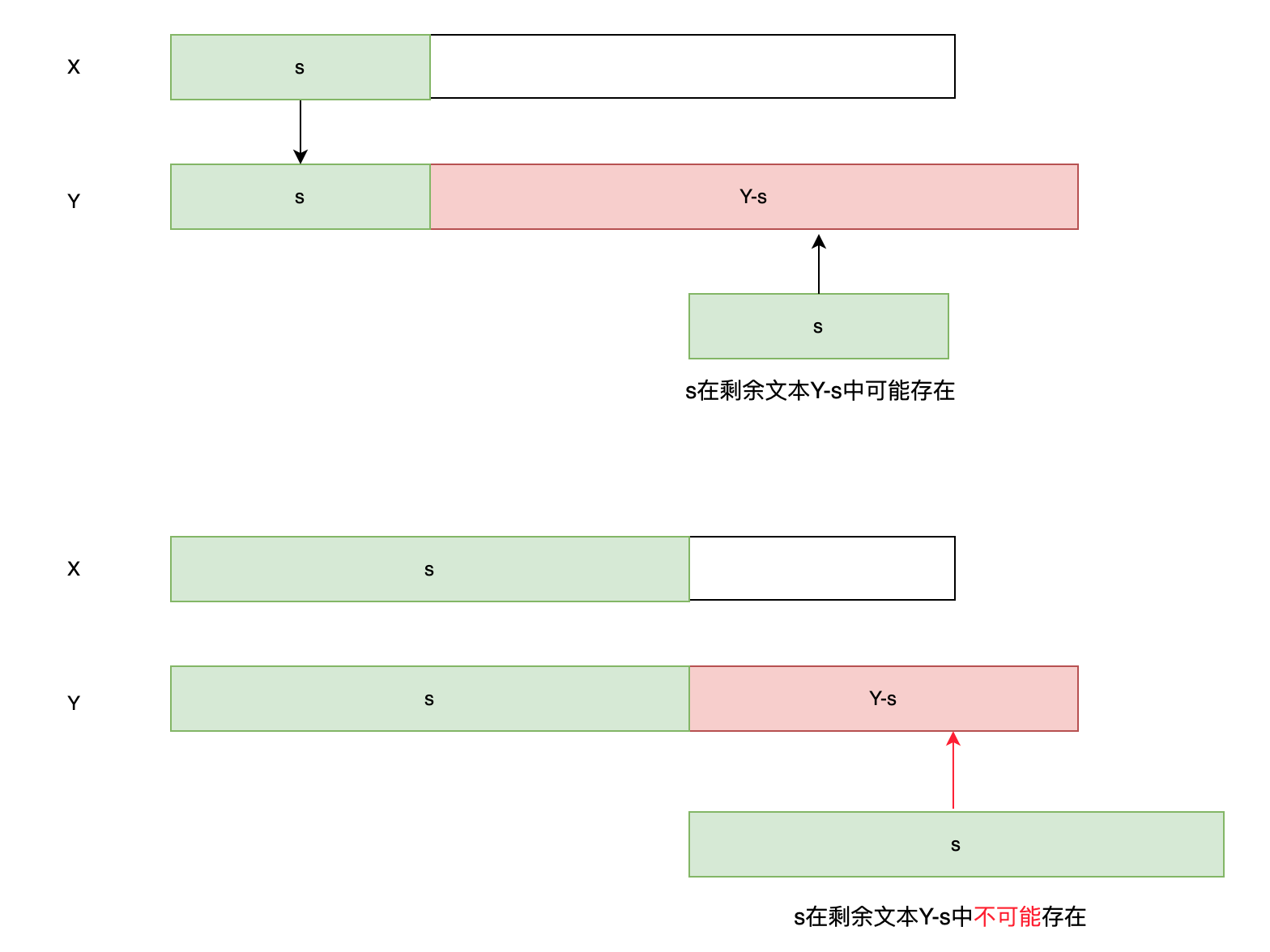
在我们自己实现的过程中,遇到了两个问题:如果我们选中的文本,在另一个文本中命中两次的话,无法确认应该取哪一个作为正确答案。那么是否可以通过 控制某个变量,来达到我们只可能命中一次的目的呢?答案是肯定的,这个变量就是长度,而临界值就是半长。
- 如果相同的文本s,不足另一段文本的一半,那么在剩余的未命中的文本中依然可能存在s,有答案不唯一的可能性
- 如果相同的文本s,超过另一段文本的一半,那么在剩余的未命中的文本中,不可能再存在s
如何快速的找到这个子串呢
在已知存在一个超过半长的子串存在时,如果快速的找到他呢?又如何确认他的具体长度呢? 可以通过轮询的方式:从X的开始位置pos=0取一半的长度,到Y中查询一次,未命中则从pos=1的位置取一半的长度,再到Y中查询一次。这样,最少一次,最多 len(Y)/2 次,就能找到这个子串。还有更快的方式吗?有。
如图所示,在轮询的过程中无论我们在什么地方取一半的长度的子串,它要么包含片段2,要么包含片段3。
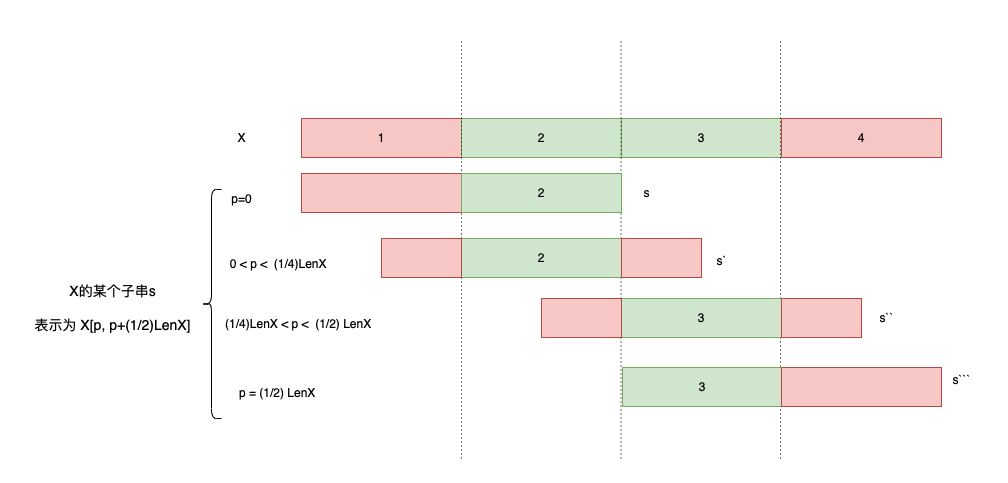
到此为止,我们可以梳理处这样一个推导过程:
- 如果两段文本存在一个公共字串,且这个公共字串的长度,大于较长字符的一半,那么这个子串必然是唯一的,他一定是的"最长公共子序列"的一部分。
- 一段文本的半长,必然包含四等分后的第二段或第三段
将这推导反过来,我们优先检查片段2、3是否在另一个文本中存在,如果不是,那么就不存在这样的半长子串;如果是,则需要进一步检查这两个 片段中,加上他们前后相同的部分后,是否超过一半。这样就可以快速且准确的找到最长公共子序列的大部分。而剩下的部分,也可以通过循环这个过程来找全,而且运算规模是不断缩小的。这就是google关于"最长公共子序列"优化的实现。
三 diff的保存
在解决两段文本进行对比的问题后,我们来着手解决第二个问题,如何进行数据的保存。如果是保存修改前后的完整内容,仅仅需要注意区分各个版本内容的顺序即可。 如果是只保存差异部分,那么还需要定义一下具体需要保存的内容与格式。
当进行完对比后,可以将对比结果分为三种类型的文本:
- 存在于两段文本的相同部分,标记为
equal - 仅存在于修改前的文本,标记为
delete - 仅存在于修改后的文本,标记为
add
修改记录:Hello, God! => Hello, Mama!
[
{
"Type": "equal",
"Text": "Hello, "
},
{
"Type":"delete",
"Text":"God"
},
{
"Type": "add",
"Text": "Mama"
},
{
"Type":"equal",
"Text":"!"
}
]
由于我们本来就需要保存修改后的完整内容,而标记为 equal 的部分,肯定存在,所以这部分的数据属于重复内容,不需要额外保存。 此外,标记为 add 的文本也存在于修改后的文本中,但依然需要特殊标记;最后,标记为 delete 的文本,在修改后的文本中已经不存在了, 所以必须保存。我们将修改前后的内容分别记录为 C1/C2,C1/C2 之间的差异记录为 diff,可以表示为:
1、C2 - C1 = diff
2、C1 + diff = C2
3、C2 - diff = C1
第一个公式表示的是计算出 diff 的过程;第二个公式表示的是通过 C1 和 diff,推导出 C2 内容的过程,在进行这个计算的过程中,除了 已知的内容 C1、diff 之外,还需要知道 diff 中的 add/delete 片段,在 C1 中的位置; 第三个公式表示的是通过 C2 和 diff,反推出 C1内容的过程, 同样,这个过程需要知道 diff 中的 add/delete 片段,在 C2 中的位置信息,所以 diff 的数据结构可以记录如下:
修改记录:Hello, God! => Hello, Mama!
[
{
"PosC1":7,
"PosC2":7,
"Type":"delete",
"Text":"God"
},
{
"PosC1":10,
"PosC2":7,
"Type": "add",
"Text": "Mama"
}
]
有了这些信息之后,就可以完成反推还原的过程,但仍然需要一个校验位来确保数据的正确性,用于验证 diff 是否真的是 C1 与 C2 的差异。 由于我们的方案是保存最新版本的内容,也就是 C2, 因此在使用中,首先需要考虑用到的是公式3 C2 - diff = C1, 需要验证这个步骤的正确性, 就需要在 C2 与 diff 之间建立联系,比如将 C2 的 md5 值随 diff 一起保存,在执行公式3前,先比较 C2 的 md5 值与保存的是否一致,如果不一致,说明 C2 与 diff 至少有一个是错误的, 也就不能得到正确的 C1,那么最终diff的结构就是:
修改记录:Hello, God! => Hello, Mama!
{
"diff":[
{
"PosC1":7,
"PosC2":7,
"Type":"delete",
"Text":"God"
},
{
"PosC1":10,
"PosC2":7,
"Type": "add",
"Text": "Mama"
}
],
"hash":"8c5f6fff8aa96f9a5e075ee257669e55"
}
在最终展示给用户时,我们通过保存的最新内容,与最新的修改,进行恢复历史版本运算,得到修改前后的 diff 标记片段,然后渲染成不同的样式,最终得到的上线后的效果如图

四 扩展话题
4.1 行对比和分组
看过 go-diff 包的源码后就知道,进行对比时,可以选择对比模式为按行对比,或按字符对比。按行对比在实际中的运用非常多,比如版本管理工具 git 就是行对比的, 一个代码文件可能有成千上万的字符,但行数可能只有几百行,这就是行对比的优势,可以缩小对比目标的规模。从对比字符到对比行的转化,就是就对对比目标进行 了一次预分组。如果我们有其他场景下,需要计算差异的需求,可以优先根据使用场景来定义预分组的规则,缩小对比范围,优化性能。比如在小说章节这类自然语言 的领域,可以考虑通过句子来进行分组。
4.2 历史快照版本
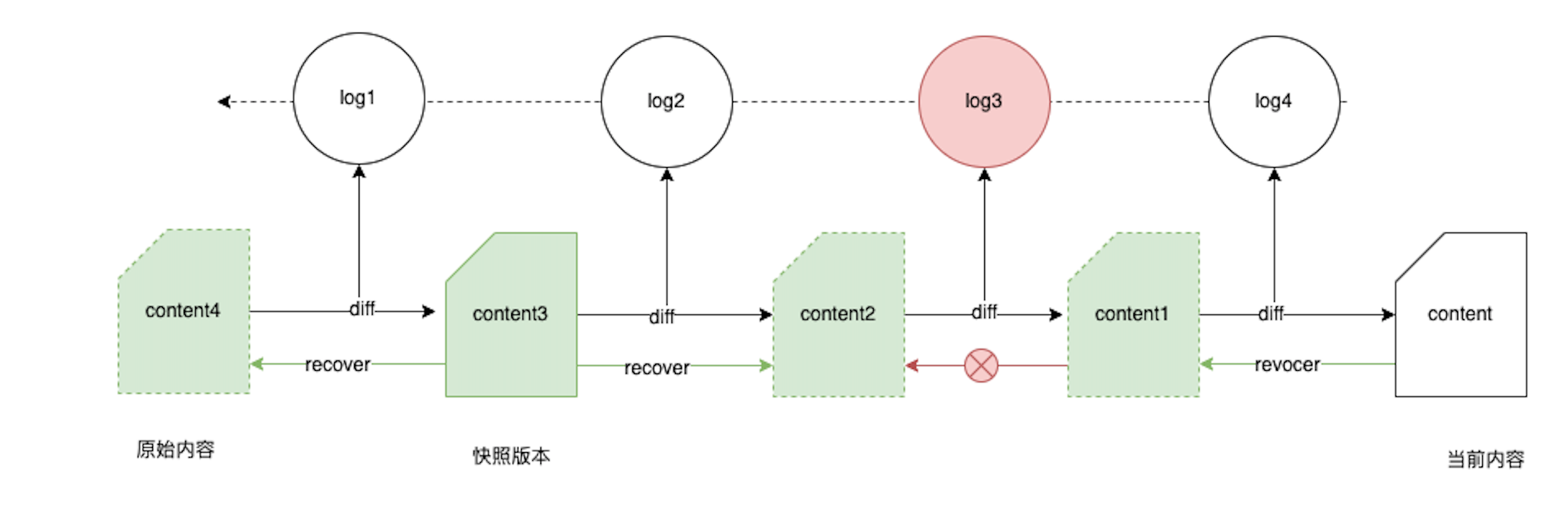
在讨论数据保存方案时,通过以 diff 数据保存为主,历史版本为辅的方案可能更优秀。保存 diff 数据的主要优势在于内容小,节省存储。然而如果出现换章的情况,整个 章节的内容都被替换掉了,那么 diff 实际上保存的是修改前后的内容和。在这种情况下,仅保存历史版本反而会更节省存储。
正常情况下的历史版本记录与恢复表示如图
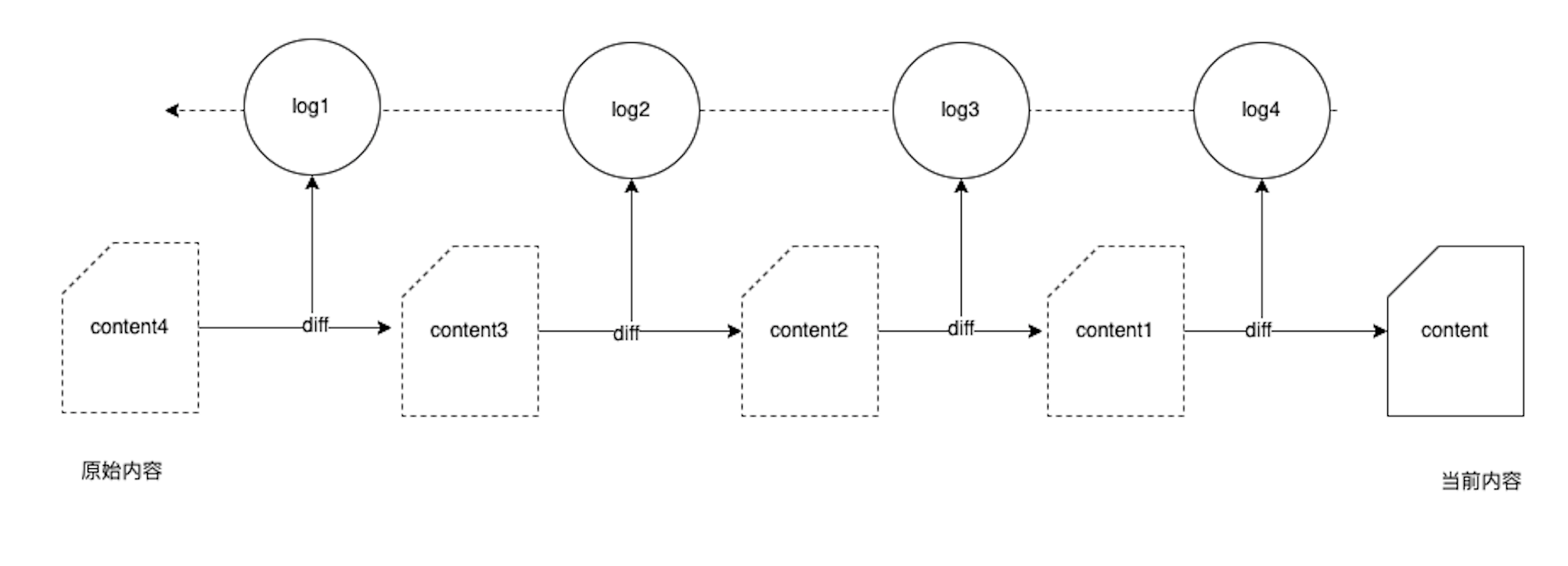
考虑记录 diff 数据的另一个缺陷:如果中间某个版本意外丢失,会导致往前的记录都变成无效的。
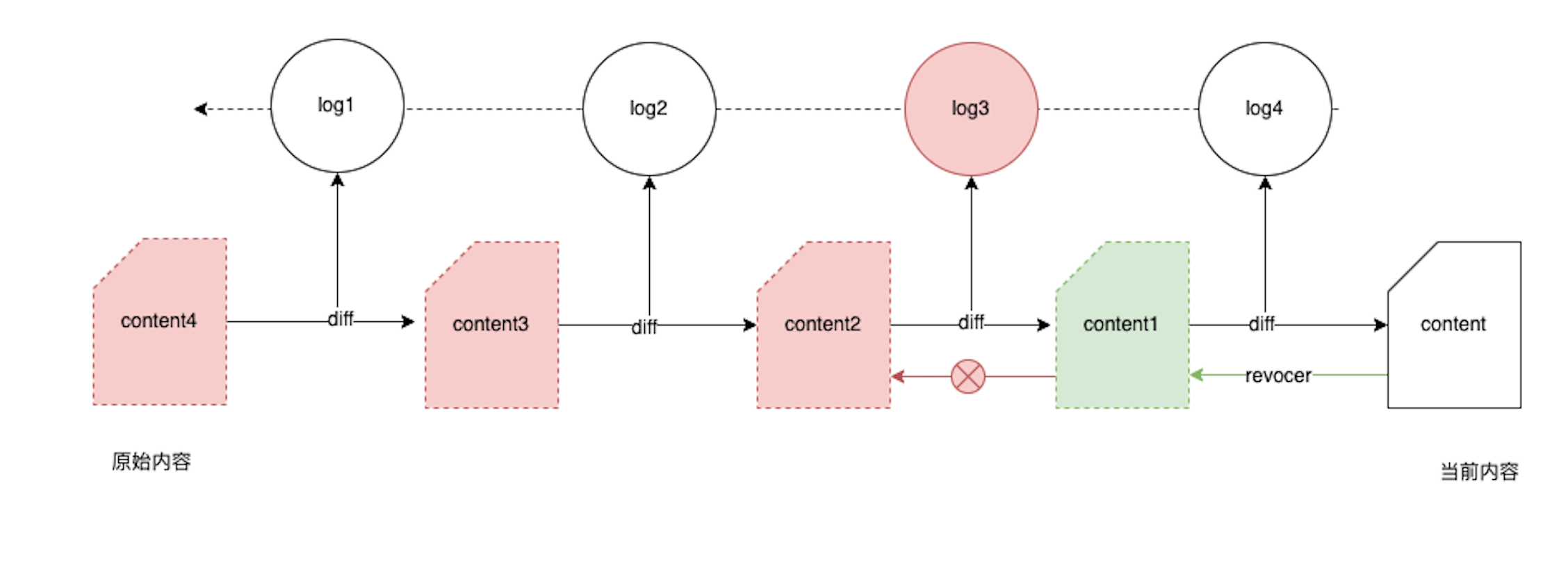
那么,自然可以想到,保存的历史版本可以包含两类记录,一类仅记录 diff 的细节,当修改的内容比较少的时候,优先考虑这种 类型的记录;另一类则是快照版本,包含完整的章节内容,当存在换章或改动内容比较多时优先考虑这种类型的记录,如果中间存在错误或丢失的 diff 记录,可以通过双向回滚的方式进行修复。